How Do We Know When to Use Which Series Test

We can use the Augmented Dickey-Fuller ADF t-statistic test to do this. However it is important that the appropriate statistical analysis is decided before starting the study at the stage of planning itself and the sample size chosen is optimum.

How To Create The Perfect Tween Study Space Study Habits Effective Study Tips School Study Tips

Plugging the given series into the integral we get.

. ADF test is a test to check whether the series has a unit root or not. If the a n are non-negative a. Strategy for Testing Series 1.

The benefit of the limit comparison test is that we can compare series without verifying the inequality we need in order to apply the direct comparison test of course at the cost of having to evaluate the limit. As shown we can write the series as a sum of two series and both of these series are convergent by the p-series test. If r 1 r.

This is the nth term test for divergence. If you see that the terms a_n do not go to zero you know the series diverges by the Divergence Test. Suppose that we have a series an a n and either an 1nbn a n 1 n b n or an 1n1bn a n 1 n 1 b n where bn 0 b n 0 for all n n.

We can use the value of r r r in the geometric series test for convergence to determine whether or not the geometric series converges. The Standard Series or one that can be handled with the integral test. Sometime the teacher gives us a single series.

Use a histogram if you need to present your results to a non-statistical public. Note that e1n1 for all integers n0. Just compute the companion improper integral with the same limits of integration as the index numbers of the summation like this.

When the limit equals zero. In addition if it converges and the series starts with n0 we. To calculate the p-value we can use the adftest function from tseries library on R.

Now that we know the series is positive decreasing and continuous we can use the integral test to say whether the series converges or diverges. Alternating Series Test. Then if lim nbn 0 lim n.

Take the absolute values of the alternating converging series. Therefore we expect that sum_n1inftye1nn will diverge. -x x -x and each term is bigger than the term after it the series converges.

Some preliminary algebraic manipulation may be required to bring the series into this form. As a statistical test to confirm your hypothesis use the Shapiro Wilk test. Sometime the teacher gives us a single series.

I am not sure to use DCT or LCT. If the series has the form X arn1 or X n it is a geometricseries which converges if jrj 1and diverges if j. For test of cgsserieshow do we knowuse direct comparison test or limit comparison test.

If r 1 then P a n converges absolutely if r 1 then P a n diverges if r 1 cant tell This is useful for series involving expondentials like 2n and factorials liken. If a series has positive terms and if its limit exists then the series converges if the result of the limit is less than 1 and diverges if this result is greater than 1. Telescoping series always look like sum fx1-fx so like the other series they are for a particular type of series but watch out for the series sum frac1nn1 and similar series that can be made into a telescoping series using partial fractions.

Many of the series you come across will fall into one of several basic types. I am not. The ratio test of convergence of series.

Always be careful with two of the few mistakes when solving for the Divergence Test. The geometric series test says that. Well I would try to see if I can directly compare first.

After youve determined the convergence or divergence of a series with the integral comparison test you can then use that series as a benchmark for investigating other series with the direct. This is more of an art than a science that is sometimes you have to try several things in order to find the. A n has a form that is similar to one of the above see whether you can use the comparison test.

If a series is a p-series with terms frac1np we know it converges if p1 and diverges otherwise. Use the integral test for positive decreasing functions or negative increasing functions only do not forget this condition. What test to use.

Since n 2 0 n2ne0 n 2 0 for 1 n 1leq nleqinfty 1 n we know that the series is continuous. Answer 1 of 2. If the seriess limit is not equal to zero or does not exist then the series is divergent.

Try comparing it to the divergent harmonic series sum_n1infty1n to show this with the limit comparison test so use b_n1n. The nth Term Test. B n 0 and bn b n is eventually a decreasing sequence.

Because the integral diverges the series diverges. If a series is a p-series with terms frac1np we know it converges if p1 and diverges otherwise. It is the most powerful test which should be the decisive argument.

This is usually a very easy test to use. If the new all positive term series converges then the series is absolutely convergent. Recognizing these types will help you decide which tests or strategies will be most useful in finding whether a series is convergent or divergent.

If a series is a geometric series with terms arn we know it converges if r. If the individual terms of a series in other words the terms of the series underlying sequence do not converge to zero then the series must diverge. Therefore since each of these series are convergent we know that the sum sumlimits_n 1infty fracn2 2n4.

When youre looking at a positive series whats the best way to determine whether it converges or diverges. When the limit equals zero the series converges. If r 1 rge1 r 1 then the series diverges.

Let a_ne1nn and b_n1n noting that a_n b_n 0 for all integers n0. If you see that the terms a_n do not go to zero you know the series diverges by the Divergence Test. If a series is a geometric series with terms arn we know it converges if r.

If a n 0 and lim n1 a n1 a n r then 8. Either both converge or both diverge. The Alternating Series Test tells us that if the terms of the series alternates in sign eg.

For test of cgsserieshow do we knowuse direct comparison test or limit comparison test. If the series is of the form X 1 np it is a p-series which we know to be convergent if p 1and divergent if. However if its not we can say that the model is stationary.

In addition if it converges and the series starts with n0 we. If it exists the series has a linear trend. As we have outlined below a few fundamental considerations will lead one to select the appropriate statistical test for hypothesis testing.

The series an a n is convergent. When testing against other distributions you cannot use Shapiro Wilk and should use for example the Anderson-Darling test or the KS test. A production of UConns Quantitative Learning CenterLearn more about us at httpqcenteruconnedu.

However it might not be easy when its expression is complicated.

The Enneagram Enthusiasts Enneagramenthusiast Instagram Photos And Videos Enneagram Type 4 Enneagram Enneagram Test

Johanna On Instagram New Series The Things I Want You To Know About Me Enneagram Edition Starting With 9 Beca Enneagram Enneagram 9 Personality Psychology

Differentiation In Writing Workshop Blog Series Tip 1 Use A Writing Pre Test Sample Writing P Differentiated Writing Teaching Writing Informational Writing

Pin On Pandas

Check Out Our Series On Disc Traits Every Manager Should Know Of Their Employees Starting With The Hig Disc Assessment Disc Personality Test Motivation Theory

Pin On Computers

Pin On Convergence

How Do We Know When We Are Done Scrum Alliance Agile Software Development Agile Development Agile

Series And Convergence Bc Calculus Unit 10 Calculus Ap Calculus Ap Calculus Ab

Your Ap Calculus Bc Students Will Use The Alternating Series Test For Convergence The Alternating Series Remainder To Appr Calculus Ap Calculus Ap Calculus Ab

My Cornell Notes Series Has Been So Unbelievably Popular I Hear From A Lot Of You Every Day A Cornell Notes Guided Reading Lesson Plans Middle School Writing

See Our Continued Series On 4 Disc Traits Every Manager Should Know Continuing With Our High I S Disc Assessment Disc Personality Test Personality Types

Pin On Math Easy Tutorials

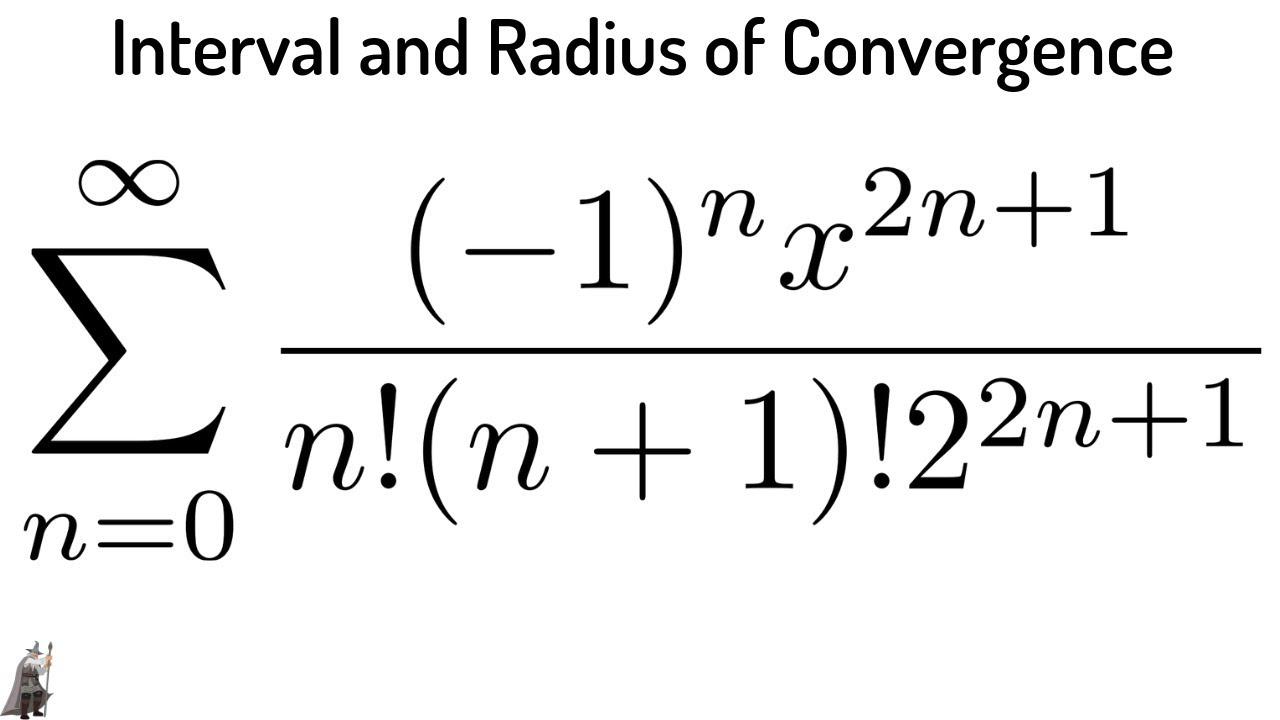
Interval And Radius Of Convergence A Power Series Using The Ratio Test F Convergence Math Videos Calculus

Series Convergence Flowchart Convergence Calculus Math

Test For Convergence Of Series Hub And Network Of Posts Convergence Sequence And Series Positive Numbers

Preparing Students For Testing School Testing School Study Tips Test Prep Strategies

Alternating Series Test Example Sum 1 N 8n 1 3n 1 Math Videos Sum Series

Sequences And Series Riddle Activity Sequence And Series Geometric Sequences Riddles